Arrays

An array is the simplest data structure. The best way to picture it is as a row of numbered parking spaces or a set of connected mailboxes.

So, an array with 10 items has indexes from 0 to 9. This index is the key to an array’s greatest strength: speed of access. If you know you want the item at index 5, you can go directly to it. It doesn’t matter if the array has 10 items or 10 million; getting the item at index 5 takes the same, tiny amount of time.

But how do we add, find, and remove items? Let’s look at the operations.

Insertion: Adding a New Item

Let’s say we have an array that can hold 50 items, but we’ve only added 10 so far. We use a separate counter variable to track that we have 10 items.

When we want to insert a new item (like the number 42), we just add it to the next empty spot. In this case, that’s index 10. Then, we increase our counter to 11.

This is super fast. It’s one simple step. We call this an \(O(1)\) operation, which is a computer science term for “constant time,” or “always fast.”

Search: Finding an Item

This is where arrays are not so great.

Imagine your array is a shopping list with 50 items, and you want to find “Milk.” The array isn’t sorted, so “Milk” could be anywhere. You have to start at index 0 (“Bread?”) and check every single item.

This is called a linear search. The time it takes to find something grows in a line with the number of items. If you have $N$ items, it takes an average of $N/2$ steps.

Deletion: Removing an Item

Deletion is the most work. It’s a two-part process:

  1. Find the Item: First, you have to search for the item you want to delete (like “Milk”). As we just saw, this is slow (average $N/2$ steps).
  2. Delete and Shift: Let’s say you find “Milk” at index 4. You can’t just leave an empty “hole” in the array. If you did, it would break your simple insert method and confuse other parts of your code. We need to keep all our items together.

To fill the hole at index 4, you must copy the item from index 5 and move it into index 4. Then you copy the item from index 6 into index 5, and so on. You must shift every item that came after the deleted item one spot to the left.

img1

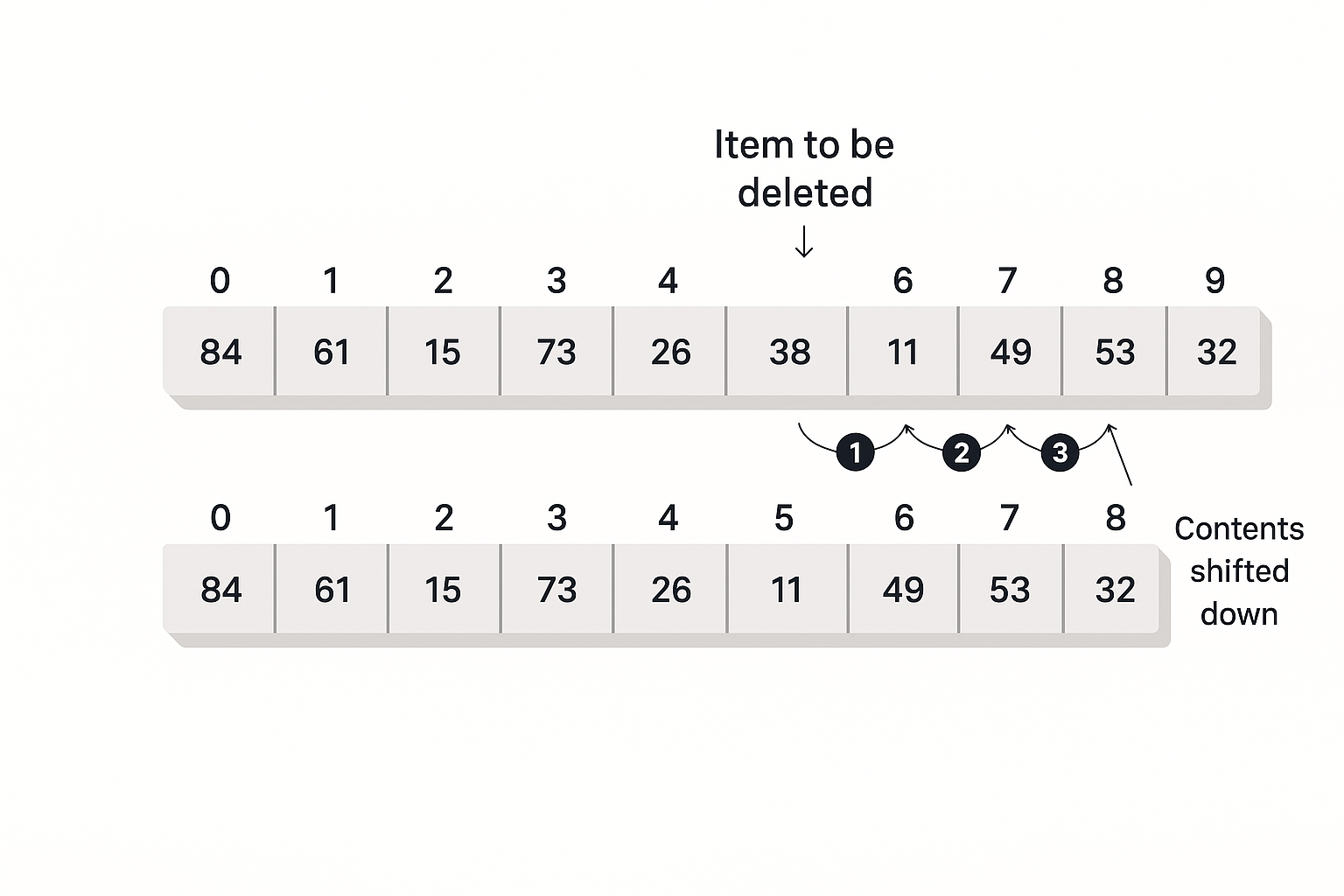
This shifting process is also very slow. If you delete the very first item (index 0), you have to move every other item in the array. This takes an average of $N/2$ moves.

So, the total time for a deletion is the slow search (average $N/2$ steps) plus the slow shift (average $N/2$ moves). In total, it’s about $N$ steps.

What About Duplicate Items?

When you build a data structure, you must decide: Are duplicates allowed?

Allowing duplicates changes how our operations work.

Searching with Duplicates

This depends on your question. Using our “quiz scores” example:

Insertion with Duplicates

Deletion with Duplicates

This also gets more complicated.

Summary of Array Speed (Big O Notation)

Here is a simple table. In computer science, we often don’t worry about the difference between $N$ (checking all items) and $N/2$ (checking half). We just call them both O(N), which means the time grows in a line with the number of items. Adding to the end is called $O(1)$, or “constant time” (always fast).

Operation No Duplicates (e.g., Student IDs) Duplicates OK (e.g., Quiz Scores)
Search (Find one) Slow - $O(N)$ (avg. $N/2$) Slow - $O(N)$ (avg. $N/2$)
Search (Find all) (Not possible) Slow - $O(N)$ (always $N$)
Insertion Slow - $O(N)$ (must search first) Slow - $O(N)$ (always $N$)
Deletion (Delete one) Slow - $O(N)$ (find + shift) Slow - $O(N)$ (find + shift)

Arrays in Java

In Java, arrays are objects. This has some important rules:

  1. You must use new: You can’t just use an array. You must first create it in memory with the new keyword. 
     int[] myScores; // This is just an empty reference (like a label)
 myScores = new int[50]; // This creates the 50 "boxes" in memory
  2. Size is Fixed: Once you create the array, you cannot change its size. Your myScores array will always have 50 spaces. If you need 51, you must create a brand new, bigger array and copy all the old data over.
  3. Default Values: When you create an int or long array, Java fills it with 0s. If you create an array of Objects (like String[]), it’s filled with a special value: null. If you try to use an item that is still null (like myStringArray[0].toLowerCase()), your program will crash with a NullPointerException.

Example Java Class

The delete() method searches for the element whose key value was passed to it as an argument and, when it finds that element, shifts all the elements in higher index cells down one cell, thus writing over the deleted value; it then decrements itemCount .

/**
 * A simple class to work with an array.
 * It doesn't allow duplicates.
 */
public class HighArray {
    private long[] array;     // This is the reference to the array
    private int itemCount;    // This counts how many items we have added

    /**
     * Constructor to create the array
     * @param max The biggest size the array can be
     */
    public HighArray(int max) {
        this.array = new long[max]; // Create the array in memory
        this.itemCount = 0;           // Start with 0 items
    }

    /**
     * Finds a specific item in the array (linear search)
     * @param searchKey The value to find
     * @return true if found, false if not
     */
    public boolean find(long searchKey) {
        int j;
        for (j = 0; j < itemCount; ++j) { // Loop from 0 to the number of items
            if (array[j] == searchKey) {  // Found it?
                break; // Stop the loop
            }
        }
        
        // If 'j' equals itemCount, the loop finished without finding a match.
        return j != itemCount; 
    }

    /**
     * Adds a new item to the end of the array
     * @param value The number to add
     */
    public void insert(long value) {
        this.array[itemCount] = value; // Put the value in the next empty spot
        itemCount++;                   // Increase the count
    }

    /**
     * Finds and deletes an item from the array
     * @param value The number to delete
     * @return true if deleted, false if not found
     */
    public boolean delete(long value) {
        int j;
        for (j = 0; j < itemCount; ++j) { // 1. Find the item
            if (array[j] == value) {
                break; // Stop the loop when we find it
            }
        }

        if (j == itemCount) {
            return false; // Didn't find it
        } else {
            // 2. Shift all items after it
            // This loop copies the item from [k+1] into [k]
            for (int k = j; k < itemCount - 1; k++) { 
                array[k] = array[k + 1];
            }

            itemCount--; // We now have one less item
            return true;
        }
    }

    /**
     * Prints all the items currently in the array
     */
    public void display() {
        // This loop only goes up to itemCount, so we don't print empty 0s
        for (int j = 0; j < itemCount; j++) {
            System.out.print(array[j] + " ");
        }
        System.out.println(""); // Add a new line at the end
    }
}